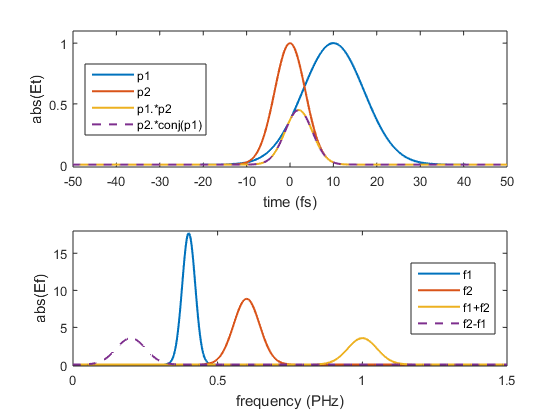
Eample of nonlinear mixing
Within the LaserPulse class, by default multiplications and divisions between pulses are done in the time domain. Multiplying two pulses then gives the sum-frequency signal. The difference frequency is obtained by multiplying the first pulse by the complex conjugate of the second.
Contents
First laser pulse
Let us define a 10fs Gaussian pulse centered at 0.4 PHz (750 nm)
% parameters n = 2^12; dt = 0.1; s = 10; t0 = 10; f0 = 0.4; t = (-n/2:n/2-1).' * dt; et = exp(-(t-t0).^2/s^2 -2i*pi*t*f0); % pulse initialization p1 = LaserPulse(t, 'fs', et);
Second laser pulse
Now let us a define a second pulse centered at a different frequency: 0.6 PHz (500 nm)
% modified parameters f0 = 0.6; et2 = exp(-(t).^2/(s/2)^2 -2i*pi*t*f0); % pulse initialization p2 = LaserPulse(t, 'fs', et2);
Sum Frequency
The sum frequency can be obtained by simple multiplication.
psf = p1 * p2 ;
Difference Frequency
The frequency difference can be obtained by multiplying the first pulse with the complex conjugate of the second.
pdf = p2 * conj(p1);
Plot pulses
figure() subplot(2,1,1) plot(p1.timeArray,p1.temporalAmplitude, ... p2.timeArray, p2.temporalAmplitude, ... psf.timeArray, psf.temporalAmplitude, ... pdf.timeArray, pdf.temporalAmplitude,'--', ... 'LineWidth', 1.5); xlabel(['time (', p1.timeUnits, ')']); ylabel('abs(Et)'); legend('p1','p2','p1.*p2', 'p2.*conj(p1)', 'location','best'); axis([-50 50 -0.02 1.1]); subplot(2,1,2) plot(p1.frequencyArray,p1.spectralAmplitude, ... p2.frequencyArray, p2.spectralAmplitude, ... psf.frequencyArray, psf.spectralAmplitude, ... pdf.frequencyArray, pdf.spectralAmplitude,'--', ... 'LineWidth', 1.5); xlabel(['frequency (', p1.frequencyUnits, ')']); ylabel('abs(Ef)'); legend('f1','f2','f1+f2','f2-f1', 'location','best'); axis([0 1.5 -0.2 18])